PROBLEMA 1 – Simulazione 28 Febbraio 2019

Riporto il testo integrale della simulazione 28 Febbraio 2019 proposta dal MIUR.

Assegnate due costanti reali a e b (con \(a>0\)), si consideri la funzione 𝑞(𝑡) così definita:

\(q(t)=at\cdot {{e}^{bt}}\)

1.  A seconda dei possibili valori di a e b, discutere se nel grafico della funzione $q(t)$ è presente un punto di massimo o di minimo. Determinare i valori di a e b in corrispondenza dei quali il grafico della funzione 𝑞(𝑡), in un piano cartesiano di coordinate (𝑡,𝑦), ha un massimo nel punto \(B\left( 2,\frac{8}{e} \right)\) 

2.  Assumendo, d’ora in avanti, di avere 𝑎=4 e 𝑏=−1/2, studiare la funzione

\[q(t)=4t\cdot {{e}^{-\frac{t}{2}}}\]

verificando, in particolare, che si ha un flesso nel punto \(F=\left( 4,\frac{16}{{{e}^{2}}} \right)\).

Determinare l’equazione della retta tangente al grafico nel punto F. 

3.  Supponendo che la funzione 𝑞(𝑡) rappresenti, per 𝑡≥0, la carica elettrica (misurata in C) che attraversa all’istante di tempo t (misurato in s) la sezione di un certo conduttore, determinare le dimensioni fisiche delle costanti 𝑎 e 𝑏 sopra indicate. Sempre assumendo 𝑎=4 e 𝑏=-1/2, esprimere l’intensità di corrente 𝑖(𝑡) che fluisce nel conduttore all’istante t; determinare il valore massimo ed il valore minimo di tale corrente e a quale valore essa si assesta col trascorrere del tempo. 

4.  Indicando, per \({{t}_{0}}\ge 0\), con \(Q\left( {{t}_{0}} \right)\) la carica totale che attraversa la sezione del conduttore in un dato intervallo di tempo \(\left[ 0,{{t}_{0}} \right]\), determinare a quale valore tende \(Q\left( {{t}_{0}} \right)\)  per  \({{t}_{0}}\to +\infty \) .

Supponendo che la resistenza del conduttore sia  \(R=3\Omega \) ,  scrivere (senza poi effettuare il calcolo), un integrale che fornisca l’energia dissipata nell’intervallo di tempo \(\left[ 0,{{t}_{0}} \right]\).   

Clicca per leggere la soluzione

PROBLEMA 2 – Simulazione 28 Febbraio 2019

Una carica elettrica puntiforme \({{Q}_{1}}=4q\) (con q positivo) è fissata nell’origine O di un sistema di riferimento nel piano  \(Oxy\) (dove x e y sono espressi in m). Una seconda carica elettrica puntiforme \({{Q}_{2}}=q\) è vincolata a rimanere sulla retta \(r\)  di equazione  \(y=1\).

1.  Supponendo che la carica \({{Q}_{2}}\) sia collocata nel punto \(A(0,1)\),  provare che esiste un unico punto  P  del piano nel quale il campo elettrostatico generato dalle cariche \({{Q}_{1}}\) e \({{Q}_{2}}\)è nullo. Individuare la posizione del punto P e discutere se una terza carica collocata in P si trova in equilibrio elettrostatico stabile oppure instabile.

2. Verificare che, se la carica \({{Q}_{2}}\) si trova nel punto della retta r avente ascissa x, l’energia potenziale elettrostatica del sistema costituito da \({{Q}_{1}}\) e \({{Q}_{2}}\) è data da

\[\mathcal{U}\left( x \right)=k\ \frac{4{{q}^{2}}}{\sqrt{1+{{x}^{2}}}}\]

dove k  è una costante positiva (unità di misura:  \(N\cdot {{m}^{2}}/{{C}^{2}}\)). 

3. Studiare la funzione \(\mathcal{U}\left( x \right)\) per \(x\in \mathbb{R}\) specificandone eventuali simmetrie, asintoti, massimi o minimi, flessi. Quali sono i coefficienti angolari delle tangenti nei punti di flesso?

4. A partire dal grafico della funzione \(\mathcal{U}\), tracciare il grafico della funzione \({\mathcal{U}}’\),  specificandone le eventuali proprietà di simmetria. Determinare il valore di \(\int_{-m}^{m}{\mathcal{U}}\prime \left( x \right)dx\) (dove m>0 indica l’ascissa del punto di minimo di \({\mathcal{U}}’\)).

Clicca per leggere la soluzione

QUESTIONARIO – Simulazione 28 Febbraio 2019

1.   Determinare i valori di a e b in modo che la funzione \(g:\mathbb{R}-\left\{ 3 \right\}\to \mathbb{R}\)

$$ g(x)=\left\{ \begin{array}{ll}3-a\ x^2 & \text{per}\ x\leq 1 \\\frac{b}{x-3} & \text{per}\ x>1\end{array} \right. $$

sia derivabile in tutto il suo dominio.  Tracciare i grafici delle funzioni g e g’.

Soluzione del quesito 1 della simulazione di maturità scientifica 28 Febbraio 2019

2.  Sia \(\mathcal{R}\) la regione piana compresa tra l’asse  e la curva di equazione \(y=2{{e}^{1-|x|}}\). Provare che, tra i rettangoli inscritti in \(\mathcal{R}\) e aventi un lato sull’asse x, quello di area massima ha perimetro minimo ed è un quadrato.

Soluzione del quesito 2 della simulazione di maturità scientifica 28 Febbraio 2019

3.  Una scatola contiene 16 palline numerate da 1 a 16.

• Se ne estraggono 3, una alla volta, rimettendo ogni volta nella scatola la pallina estratta. Qual è la probabilità che il primo numero estratto sia 10 e gli altri due minori di 10?
• Se ne estraggono 5 contemporaneamente. Qual è la probabilità che il più grande dei numeri estratti sia uguale a 13?\

Soluzione del quesito 3 della simulazione di maturità scientifica 28 Febbraio 2019

4.  Scrivere, giustificando la scelta effettuata, una funzione razionale \(y=\frac{s(x)}{t(x)}\) ,  dove s(x) e t(x)  sono polinomi, tale che il grafico della funzione:

• incontri l’asse nei punti di ascissa -1 e 2 e sia ad esso tangente in quest’ultimo punto;
• abbia asintoti verticali di equazioni  x=-3 e x=1 ;
• passi per il punto P(7,10) .

Rappresentare, qualitativamente, il grafico della funzione trovata.

Soluzione del quesito 4 della simulazione di maturità scientifica 28 Febbraio 2019

5.  Si consideri la superficie sferica  di equazione \({{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2x+6z=0\).

• Dopo aver determinato le coordinate del centro e la misura del raggio, verificare che il piano di equazione π: \(3x-2y+6z+1=0\) e la superficie S sono secanti.
• Determinare il raggio della circonferenza ottenuta intersecando π e S .

Soluzione del quesito 5 della simulazione di maturità scientifica 28 Febbraio 2019

6.  Un punto materiale si muove di moto rettilineo, secondo la legge oraria espressa, per \(t\ge 0\),  da
\(x\left( t \right)=\frac{1}{9}{{t}^{2}}\left( \frac{1}{3}t+2 \right)\) dove x(t) indica (in metri) la posizione occupata dal punto all’istante t (in secondi). Si tratta di un moto uniformemente accelerato? Calcolare la velocità media nei primi 9 secondi di moto e determinare l’istante in cui il punto si muove a questa velocità.

Soluzione del quesito 6 della simulazione di maturità scientifica 28 Febbraio 2019

7.  Una sfera di massa \(m\) urta centralmente a velocità \(v\) una seconda sfera, avente massa \(3m\) ed inizialmente ferma.

a.  Stabilire le velocità delle due sfere dopo l’urto, nell’ipotesi che tale urto sia perfettamente elastico.

b.  Stabilire le velocità delle due sfere dopo l’urto, nell’ipotesi che esso sia completamente anelastico. Esprimere, in questo caso, il valore dell’energia dissipata.

Soluzione del quesito 7 della simulazione di maturità scientifica 28 Febbraio 2019

8.  Un campo magnetico, la cui intensità varia secondo la legge , dove 𝑡 indica il tempo, attraversa perpendicolarmente un circuito quadrato di lato 𝑙. Detta 𝑅 la resistenza presente nel circuito, determinare la forza elettromotrice e l’intensità di corrente indotte nel circuito all’istante 𝑡. Specificare le unità di misura di tutte le grandezze coinvolte.

Soluzione del quesito 8 della simulazione di maturità scientifica 28 Febbraio 2019

Soluzione Problema 1 Simulazione 28 Febbraio 2019

Soluzione prima domanda

Osserviamo subito che la funzione è definita su tutto l’asse dei reali (il dominio è tutto \(\mathbb{R}\)).

Per individuare eventuali punti di massimo e minimo della funzione, bisogna studiare il segno della derivata prima:

${q}'(t)=(a+abt){{e}^{bt}}=a\left( 1+bt \right){{e}^{bt}}>0$

Considerato che $a>0$ e che l’esponenziale è una funzione sempre positiva, il segno della disequazione dipende soltanto da $1+bt$.

Caso b>0: Si ha che \(1+bt>0\) \( \Rightarrow \) \(t>-\frac{1}{b}\)

In questo caso la funzione presenta un minimo in corrispondenza di t=-1/b.

Caso b<0: Si ha che \(1+bt>0\) \(\Rightarrow\) \(t<-\frac{1}{b}\)

In questo caso la funzione presenta un massimo in corrispondenza di t=-1/b.

Affinché la funzione presenti un massimo in B, si deve avere che b<0, \(t=-\frac{1}{b}=2\) \(\Rightarrow \) \(b=-\frac{1}{2}\).

In corrispondenza di t=2 inoltre la funzione deve valere \(\frac{8}{e}\):

\(q(2)=2a\cdot {{e}^{2b}}=2a\cdot {{e}^{-1}}=\frac{2a}{e}=\frac{8}{e}\) \(\Rightarrow \)  \(a=4\)

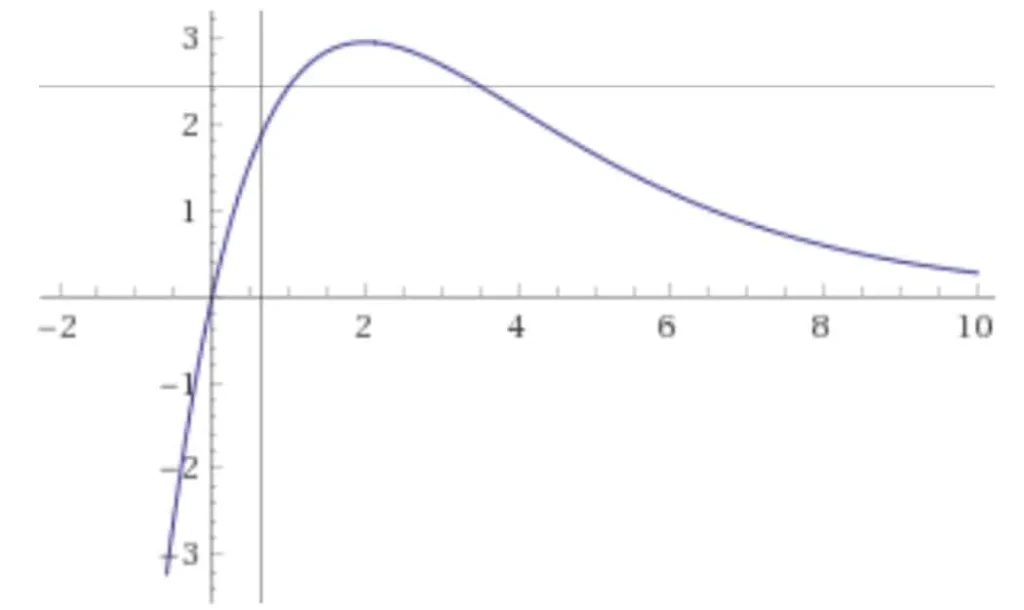
Soluzione seconda domanda

La funzione è definita su tutto\(\mathbb{R}\) ed inoltre ha un punto di massimo in \(B\left( 2,\frac{8}{e} \right)\).

È crescente per t<2, e risulta decrescente per t>2.

Studio il segno della funzione:

\(q(t)>0\) \(\Rightarrow \) \(t>0\).

Procediamo con il calcolo dei limiti:

\(\underset{t\to +\infty }{\mathop{\lim }}\,\frac{4t}{{{e}^{\frac{t}{2}}}}=\frac{\infty }{\infty }=0\)  (si tratta di una forma indeterminata, risolvibile considerando che il denominatore tende ad infinito come un esponenziale).

\(\underset{t\to -\infty }{\mathop{\lim }}\,\frac{4t}{{{e}^{\frac{t}{2}}}}=\frac{-\infty }{{{0}^{+}}}=-\infty \)

Per concludere passiamo allo studio del segno della derivata seconda ed individuiamo la presenza di eventuali punti di flesso:

\({q}”(t)=\left( -4+t \right)\cdot {{e}^{-\frac{t}{2}}}>0\) \(\Rightarrow \) \(t>4\)

Quindi la funzione è convessa per t>4 e concava per t<4, presenta inoltre un punto di flesso in corrispondenza di t=4, si ha:

\(q(4)=16\cdot {{e}^{-2}}\) \(\Rightarrow \) \(F=\left( 4,\frac{16}{{{e}^{2}}} \right)\)

La retta tangente nel punto F ha equazione:

\(y={q}’\left( 4 \right)\left( t-4 \right)+\frac{16}{{{e}^{2}}}\), dove \({q}’\left( 4 \right)=-\frac{4}{{{e}^{2}}}\)

Soluzione terza domanda

Le costanti a e b con le relative unità di misura sono: \(a=4\,C\) , \(b=-\frac{1}{2}{{s}^{-1}}\).

La corrente elettrica i(t) è la derivata rispetto al tempo della carica che fluisce attraverso la sezione del conduttore.

\(i\left( t \right)={q}'(t)=4\left( 1-\frac{1}{2}t \right)\cdot {{e}^{-\frac{1}{2}t}}\)

Per il calcolo delle correnti massime e minime, si procede allo studio del segno della derivata prima, che però coincide con lo studio del segno della derivata seconda di q(t).

\({i}'(t)={q}”\left( t \right)\) \(\Rightarrow\) \(t<4\).

L’intensità della corrente vale \(i\left( 0 \right)=4\,A={{i}_{\max }}\) all’istante iniziale, poi diminuisce fino a raggiungere il suo picco minimo all’istante t=4s, \(i\left( 4 \right)=-\frac{4}{{{e}^{2}}}\,A={{i}_{\min }}\), per poi risalire verso un asintoto orizzontale e stabilizzarsi al valore limite:

\(\underset{t\to +\infty }{\mathop{\lim }}\,i(t)=0\)

Soluzione quarta domanda

La carica che attraversa il conduttore nell’intervallo \(\left[ 0,{{t}_{0}} \right]\) è data dall’integrale:

\(Q\left( {{t}_{0}} \right)=\int\limits_{0}^{{{t}_{0}}}{i(t)dt}=\int\limits_{0}^{{{t}_{0}}}{{q}'(t)dt}=\left[ q(t) \right]_{0}^{{{t}_{0}}}=q\left( {{t}_{0}} \right)\)

Per \({{t}_{0}}\to \infty \) si ha che \(\underset{{{t}_{0}}\to +\infty }{\mathop{\lim }}\,Q\left( {{t}_{0}} \right)=0\)

Per quanto riguarda invece l’energia dissipata attraverso la resistenza per effetto Joule si ha:

\(W=\underset{{{t}_{0}}\to +\infty }{\mathop{\lim }}\,\int\limits_{0}^{{{t}_{0}}}{R{{\left[ i(t) \right]}^{2}}dt}=\underset{{{t}_{0}}\to +\infty }{\mathop{\lim }}\,16R\int\limits_{0}^{{{t}_{0}}}{{{\left( 1-\frac{1}{2}t \right)}^{2}}\cdot {{e}^{-t}}dt}\)

Soluzione Problema 2 Simulazione 28 Febbraio 2019

Soluzione prima domanda

In qualunque punto diverso dall’asse delle y, il campo elettrico non può annullarsi.

Il campo elettrico è la somma di due campi elettrici radiali alle rispettive cariche. Perché il campo possa annullarsi, i due vettori devono essere diretti lungo la stessa direzione e in versi opposti e ciò accade soltanto lungo il segmento OA (tenuto conto che le cariche hanno lo stesso segno).

Il punto in cui si annulla è P(0,y) con 0<y<1 e si ottiene uguagliando i campi elettrici generati dalle due cariche:

\({{E}_{1}}(y)={{E}_{2}}(y)\Rightarrow \frac{1}{4\pi {{\varepsilon }_{0}}}\frac{4q}{{{y}^{2}}}=\frac{1}{4\pi {{\varepsilon }_{0}}}\frac{q}{{{\left( 1-y \right)}^{2}}}\Rightarrow 4{{\left( 1-y \right)}^{2}}={{y}^{2}}\Rightarrow 3{{y}^{2}}-8y+4=0\)

L’equazione di secondo grado fornisce due soluzioni, di cui una soltanto è compresa nell’intervallo (0,1) e vale y=2/3.

Il punto cercato è \(P\left( 0,\frac{2}{3} \right)\)

Una carica Q posta nel punto P(0, 2/3) si trova in un punto di equilibrio instabile. Se una terza carica positiva Q , posta nel punto P, viene allontanata di pochissimo dal punto P, tende ad allontanarsi ancora di più. La carica nel punto P ha un massimo di energia potenziale e quindi tende a spostarsi in punti di minor energia potenziale. Una terza carica Q negativa, posta in P si troverebbe anch’essa in equilibrio elettrostatico instabile. Se Q viene allontanata di pochissimo dal punto P, nella direzione dell’asse y¸ tende a muoversi verso la carica più vicina e non tornerebbe nel punto P.

Soluzione seconda domanda

La distanza tra le due cariche può essere calcolata attraverso il teorema di Pitagora e vale \(r=\sqrt{1+{{x}^{2}}}\).

L’energia potenziale generata da una coppia di cariche è data da \(\mathcal{U}=\frac{1}{4\pi {{\varepsilon }_{0}}}\frac{{{q}_{1}}{{q}_{2}}}{r}\)

Da cui sostituendo le espressioni della distanza r tra le due cariche e i valori delle rispettive cariche si ha che \(\mathcal{U}\) è una funzione di x e vale:

\(\mathcal{U}\left( x \right)=\frac{1}{4\pi {{\varepsilon }_{0}}}\frac{4{{q}^{2}}}{\sqrt{1+{{x}^{2}}}}\) e \(k=\frac{1}{4\pi {{\varepsilon }_{0}}}\)

Soluzione terza domanda

\(\mathcal{U}\left( x \right)=k\ \frac{4{{q}^{2}}}{\sqrt{1+{{x}^{2}}}}\)

È una funzione definita su tutto \(\mathbb{R}\), in quanto \(1+{{x}^{2}}\ge 0\,\forall x\in \mathbb{R}\) Studiamo il segno della funzione: \(\mathcal{U}\left( x \right)=k\ \frac{4{{q}^{2}}}{\sqrt{1+{{x}^{2}}}}>0\,\,\forall x\in \mathbb{R}\)

È una funzione pari, infatti \(\mathcal{U}\left( -x \right)=k\ \frac{4{{q}^{2}}}{\sqrt{1+{{\left( -x \right)}^{2}}}}=k\ \frac{4{{q}^{2}}}{\sqrt{1+{{x}^{2}}}}=\mathcal{U}\left( x \right)\)

\(\underset{x\to \pm \infty }{\mathop{\lim }}\,k\ \frac{4{{q}^{2}}}{\sqrt{1+{{x}^{2}}}}=0\)

Quindi presenta un asintoto orizzontale bilatero di equazione y=0.

Studiamo il segno della derivata prima della funzione:

\({\mathcal{U}}’\left( x \right)=k{{q}^{2}}\ \frac{-4x}{\sqrt{{{\left( 1+{{x}^{2}} \right)}^{3}}}}>0\,\Rightarrow \,x<0\)

La funzione è crescente per x>0 e decrescente per x<0. Presenta un punto di massimo relativo ed assoluto in corrispondenza di \(\left( 0,\mathcal{U}\left( 0 \right) \right)=\left( 0,4k{{q}^{2}} \right)\).

Studiamo il segno della derivata seconda:

\({\mathcal{U}}”\left( x \right)=k{{q}^{2}}\ \frac{8{{x}^{2}}-4}{\sqrt{{{\left( 1+{{x}^{2}} \right)}^{5}}}}>0\,\Rightarrow \,x<-\frac{1}{\sqrt{2}}\vee x>\frac{1}{\sqrt{2}}\)

La funzione è concava per valori interni all’intervallo \(\left( -\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}} \right)\) e convessa per valori esterni. Presenta punti di flesso in \(x=\pm \frac{1}{\sqrt{2}}\) .

A questo punto cerchiamo calcoliamo i coefficienti angolari delle rette tangenti nei punti di flesso:

\({\mathcal{U}}’\left( \pm \frac{1}{\sqrt{2}} \right)=\ \mp \frac{8\sqrt{3}k{{q}^{2}}}{9}\)

Soluzione quarta domanda

Poiché \(\mathcal{U}\left( x \right)\) è una funzione pari, \({\mathcal{U}}’\left( x \right)\) sarà sicuramente una funzione dispari, infatti:

Infatti poiché \(\mathcal{U}\left( x \right)\) è pari e derivabile su tutto \(\mathbb{R}\), si avrà che \(\mathcal{U}\left( -x \right)=\mathcal{U}\left( x \right)\) e derivando entrambi i membri dell’equazione rispetto ad x, si ottiene \(-{\mathcal{U}}’\left( -x \right)={\mathcal{U}}’\left( x \right)\).

Si ha che \(\mathcal{U}\left( x \right)\) è crescente in x<0, quindi \({\mathcal{U}}’\left( x \right)\) è positiva per ogni valore di x negativo.

Inoltre \(\mathcal{U}\left( x \right)\) è decrescente in x>0, quindi \({\mathcal{U}}’\left( x \right)\) è negativa per ogni valore di x negativo.

Il grafico ha pendenza orizzontale in x=0 e per \(x\to \pm \infty \), quindi  \({\mathcal{U}}’\left( x \right)\) per x=0 passa dall’origine e \({\mathcal{U}}’\left( x \right)\to 0\) per \(x\to \pm \infty \) (quindi y=0 è asintoto orizzontale per \({\mathcal{U}}’\left( x \right)\)).

In base alle deduzioni fatte sulla derivata della funzione \(\mathcal{U}\left( x \right)\), è possibile tracciare un possibile grafico, come quello in figura.

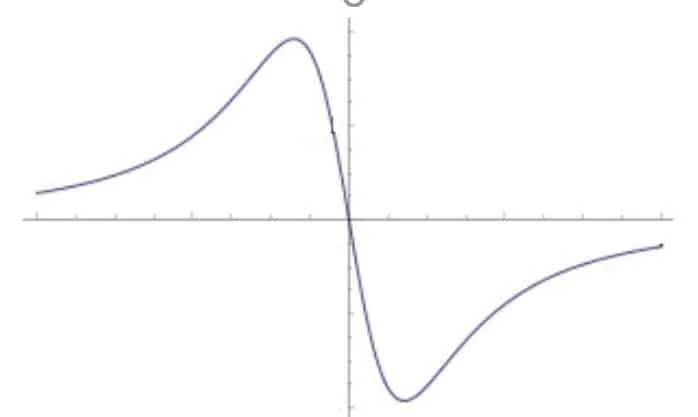
\(\int_{-m}^{m}{\mathcal{U}}\prime \left( x \right)dx=\left[ \mathcal{U}(x) \right]_{-m}^{m}=\) \(\mathcal{U}(m)-\mathcal{U}(-m)=2\mathcal{U}(m)=\) \(\mathcal{U}\left( x \right)=k\ \frac{8{{q}^{2}}}{\sqrt{1+{{m}^{2}}}}\)

SOLUZIONE QUESITI

Soluzione Quesito 1 – Simulazione 28 Febbraio 2019

Perché la funzione sia derivabile, deve essere innanzi tutto continua, quindi come prima cosa imponiamo la continuità della funzione g(x).

\(\underset{x\to {{1}^{+}}}{\mathop{\lim }}\,g(x)=\underset{x\to {{1}^{+}}}{\mathop{\lim }}\,\frac{b}{x-3}=-\frac{b}{2}\)

\(\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,g(x)=\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,3-a\ {{x}^{2}}=3-a=g(1)\)

Per la continuità il limite destro e sinistro devono entrambi coincidere con il valore della funzione nel punto di ascissa x=1, quindi \(-\frac{b}{2}=3-a\) \(\Rightarrow \) \(a=3+\frac{b}{2}\)

A questo punto imponiamo che il limite del rapporto incrementale esiste ed è finito.

\(\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{g(1+\Delta x)-g(1)}{\Delta x}=m\in \mathbb{R}\) \(\Rightarrow \) \(m=\underset{\Delta x\to {{0}^{+}}}{\mathop{\lim }}\,\frac{g(1+\Delta x)-g(1)}{\Delta x}=\) \(\underset{\Delta x\to {{0}^{-}}}{\mathop{\lim }}\,\frac{g(1+\Delta x)-g(1)}{\Delta x}\)

Calcoliamo il limite destro:

\(\underset{\Delta x\to {{0}^{+}}}{\mathop{\lim }}\,\frac{g(1+\Delta x)-g(1)}{\Delta x}=\) \(\underset{\Delta x\to {{0}^{+}}}{\mathop{\lim }}\,\frac{\frac{b}{-2+\Delta x}+\frac{b}{2}}{\Delta x}=\) \(\underset{\Delta x\to {{0}^{+}}}{\mathop{\lim }}\,\frac{b\Delta x}{\Delta x\left( -2+\Delta x \right)2}=\) \(\underset{\Delta x\to {{0}^{+}}}{\mathop{\lim }}\,\frac{b}{\left( -2+\Delta x \right)2}=-\frac{b}{4}\)

Calcoliamo anche il limite sinistro:

\(\underset{\Delta x\to {{0}^{-}}}{\mathop{\lim }}\,\frac{g(1+\Delta x)-g(1)}{\Delta x}=\) \(\underset{\Delta x\to {{0}^{-}}}{\mathop{\lim }}\,\frac{3-a\ {{(1+\Delta x)}^{2}}-3+a}{\Delta x}=\) \(\underset{\Delta x\to {{0}^{-}}}{\mathop{\lim }}\,a\left[ \frac{-\ {{(1+\Delta x)}^{2}}+1}{\Delta x} \right]=\) \(-a\underset{\Delta x\to {{0}^{-}}}{\mathop{\lim }}\,\left[ \frac{\ {{(1+\Delta x)}^{2}}-1}{\Delta x} \right]=-2a\)

A questo punto uguagliamo limite destro e sinistro e otteniamo una seconda condizione da mettere a sistema con la prima:  \(\Rightarrow \) \(b=8a\)

Per concludere otteniamo il sistema con la condizione di continuità (condizione necessaria alla derivabilità) e dell’esistenza finita del rapporto incrementale (condizione sufficiente alla derivabilità)

$$\left\{\begin{align*}a &= 3 + \frac{b}{2} \\b &= 8a\end{align*}\right.$$

$$\left\{\begin{align*}a &= -1 \\b &= -8\end{align*}\right.$$

Soluzione Quesito 2 – Simulazione 28 Febbraio 2019

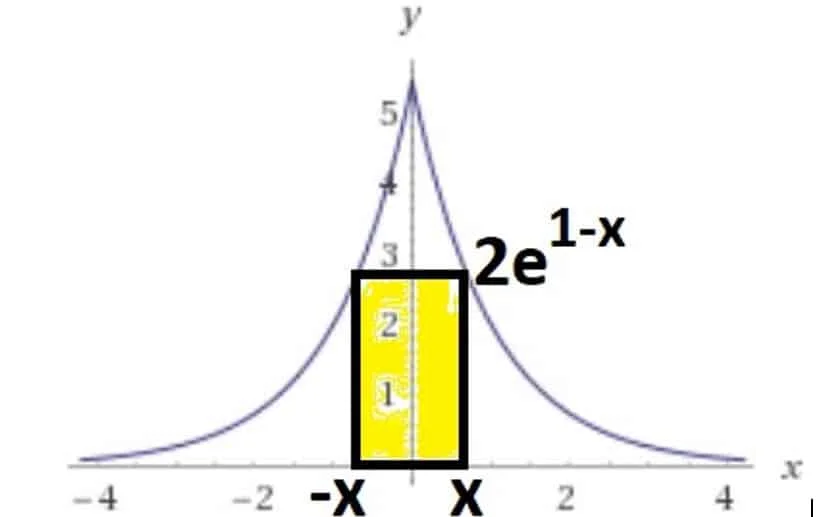
La funzione \(y=2{{e}^{1-|x|}}\) è una funzione pari.

Per x>0 possiamo togliere il valore assoluto e vale \(y=2{{e}^{1-x}}=2e\cdot {{e}^{-x}}\) che coincide con il grafico di \({{e}^{-x}}\) moltiplicato per una costante.

Quindi per x>0 costruiamo un grafico che va come \({{e}^{-x}}\), mentre per x<0 specchiamo il grafico rispetto all’asse delle y e così possiamo rappresentare graficamente un generico rettangolo \(\mathcal{R}\) che rispetta le condizioni imposte dal quesito.

Il rettangolo \(\mathcal{R}\) ha base \(b=2x\), con \(x>0\) e altezza \(h=2e\cdot {{e}^{-x}}\), da cui si ottiene che la sua area vale \(A(x)=b\cdot h=4ex\cdot {{e}^{-x}}\)

L’area massima si ottiene cercando il massimo valore della funzione A(x), ovvero studiando il segno della derivata prima della funzione:

\({A}'(x)=4e\left( {{e}^{-x}}-x\cdot {{e}^{-x}} \right)>0\) \(\Rightarrow \) \(x<1\)

Il massimo dell’area si ottiene quando x=1 e in corrispondenza di questo punto si ha che la base vale \(b=h=2\), quindi si tratta di un quadrato di lato 2.

Passiamo ora a ragionare sul perimetro: \(f(x)=2b+2h=4x+4e\cdot {{e}^{-x}}\), con x>0. Sudiamo il segno della derivata della funzione perimetro: \({f}'(x)=4-4e\cdot {{e}^{-x}}>0\) \(\Rightarrow \) \(x>1\)

Il minimo per la funzione perimetro si ha in corrispondenza di x=1, e si ottiene che corrisponde con lo stesso quadrato che ha l’area massima.

Soluzione Quesito 3 – Simulazione 28 Febbraio 2019

Caso 1

Il primo caso si tratta di tre estrazioni con reimmissione, pertanto possiamo considerare una sequenza di tre eventi indipendenti.

\(P\left( {{x}_{1}}=10 \right)=\frac{1}{16}\)

\(P\left( {{x}_{2}}<10 \right)=\frac{9}{16}\)

\(P\left( {{x}_{3}}<10 \right)=\frac{9}{16}\)

\(P\left( {{x}_{1}}=10,\,{{x}_{2}}<10,{{x}_{3}}<10 \right)=\) \(P\left( {{x}_{1}}=10)\cdot P({{x}_{2}}<10)\cdot P({{x}_{3}}<10 \right)=\) \(\frac{1}{16}\cdot \frac{9}{16}\cdot \frac{9}{16}\simeq 0,02=2\%\).

Caso 2

Numero di quintuple ordinate con 4 numeri minori di 13 seguiti dal 13 (a-b-c-d-13): $\binom{12}{4}$

Numero di quintuple ordinate con i numeri da 1 a 16 (a-b-c-d-e): $\binom{16}{5}$

Il rapporto tra le combinazioni favorevoli e le possibili combinazioni ci dà la probabilità cercata:

$$ p = \frac{\binom{12}{4}}{\binom{16}{5}} = \frac{3 \times 5 \times 11}{7 \times 13 \times 16} \approx 0.1133 = 11,33\%$$

Soluzione Quesito 4 – Simulazione 28 Febbraio 2019

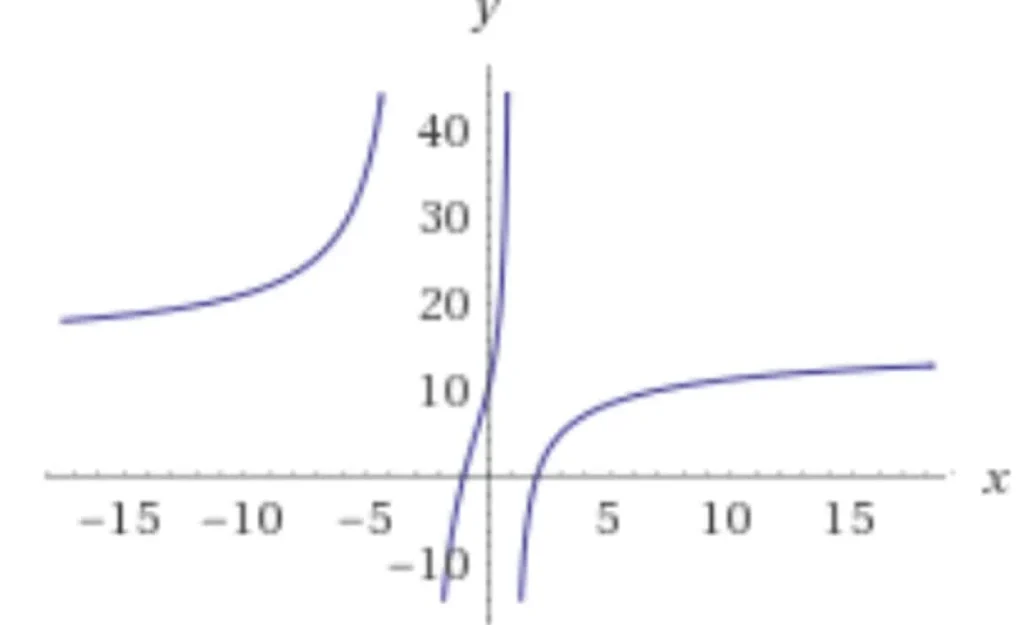
Il numeratore deve essere divisibile per (x+1) e per (x-2)² in maniera tale che s(x) e quindi y si annulli in corrispondenza dei punti di ascissa -1 e 2, ed in particolare risulti tangente al punto A(2,0). La condizione di tangenza si ottiene imponendo che il fattore (x-2) abbia molteplicità almeno pari a 2.

Il denominatore deve essere divisibile per (x+3) e per (x-1) in maniera tale che t(x)  si annulli in corrispondenza dei punti di ascissa -3 e 1.

A questo punto bisogna rispettare la terza condizione ovvero che la funzione passi per il punto P(7,10).

Scegliamo una funzione nella forma \(y=k\frac{(x+1){{(x-2)}^{2}}}{(x+3)(x-1)}\)  e andiamo ad imporre la terza condizione per determinare il valore di k.

\(10=k\frac{(7+1){{(7-2)}^{2}}}{(7+3)(7-1)}=\frac{10}{3}k\) \(\Rightarrow\) \(k=3\)

Quindi una possibile soluzione della funzione cercata è \(y=3\cdot \frac{(x+1){{(x-2)}^{2}}}{(x+3)(x-1)}\)

Soluzione Quesito 5 – Simulazione 28 Febbraio 2019

Il centro e il raggio si ottengono mediante il completamento dei quadrati:

\(\left( {{x}^{2}}-2x+1 \right)+{{y}^{2}}+\left( {{z}^{2}}+6z+9 \right)=1+9\)

In questo modo l’equazione viene riscritta nella forma

\({{\left( x-1 \right)}^{2}}+{{y}^{2}}+{{\left( z+3 \right)}^{2}}=10\)

E si deduce immediatamente che il centro della sfera è \(C(1,0,-3)\) e il raggio vale \(R=\sqrt{10}\)

A questo punto calcolo la distanza tra il piano e il centro della sfera:

\(d=\frac{\left| 3\cdot 1-2\cdot 0-3\cdot 6+1 \right|}{\sqrt{{{3}^{2}}+{{2}^{2}}+{{6}^{2}}}}=2\)

Si ha che d<R e quindi la sfera e il piano si intersecano.

Il raggio della circonferenza può essere calcolato con il teorema di Pitagora e vale:

\(r=\sqrt{{{R}^{2}}-{{d}^{2}}}=\sqrt{6}\)

Soluzione Quesito 6 – Simulazione 28 Febbraio 2019

Il moto è uniformemente accelerato se l’accelerazione è costante. L’accelerazione è data dalla derivata seconda della legge oraria x(t).

\(x\left( t \right)=\frac{1}{27}{{t}^{3}}+\frac{2}{9}{{t}^{2}}\) \(\Rightarrow \) \(v(t)={x}'(t)=\frac{1}{9}{{t}^{2}}+\frac{4}{9}t\) \(\Rightarrow \) \(a(t)={v}'(t)=\frac{2}{9}t+\frac{4}{9}\)

L’accelerazione dipende dal tempo quindi non si può trattare di un moto uniformemente accelerato.

La velocità media si ricava dalla formula: \(\bar{v}=\frac{x({{t}_{F}})-x({{t}_{I}})}{{{t}_{F}}-{{t}_{I}}}=\) \(\frac{x(9)-x(0)}{9-0}=5m/s\)

L’istante in cui il punto si muove a questa velocità si ottiene risolvendo la seguente equazione:

\(v(t)=\frac{1}{9}{{t}^{2}}+\frac{4}{9}t=45\) (\(t\ge 0\) )\(\Rightarrow\) \(t=5s\)

Soluzione Quesito 7 – Simulazione 28 Febbraio 2019

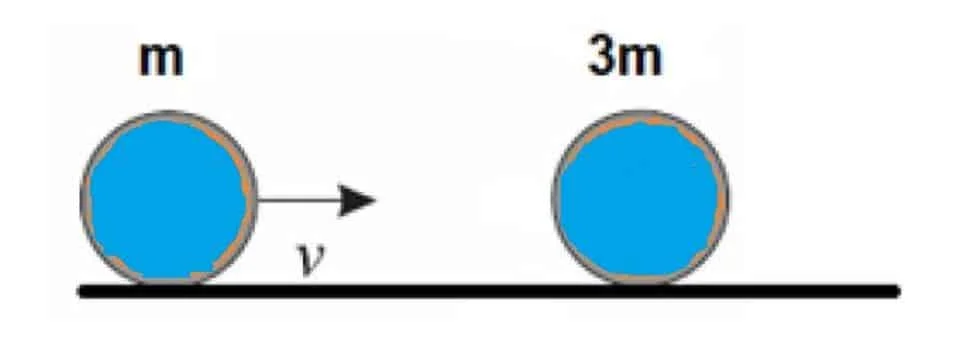
a. Nel caso di urto perfettamente elastico si conserva l’energia e la quantità di moto. Impostiamo le due equazioni:

$$\left\{\begin{align*}& \frac{1}{2}mv^2 = \frac{1}{2}m{v_1}^2 + \frac{1}{2}(3m){v_2}^2 \\& mv = m{v_1} + 3m{v_2}\end{align*}\right.$$

È possibile semplificare le masse nelle equazioni e il sistema diventa:

$$\left\{\begin{align*}& v^2 = {v_1}^2 + 3{v_2}^2 \\& v = {v_1} + 3{v_2}\end{align*}\right.$$

$$\left\{\begin{align*}& v^2 = {v_1}^2 + 3{v_2}^2 \\& v^2 = {v_1}^2 + 9{v_2}^2 + 6v_1v_2\end{align*}\right.$$

$$\left\{\begin{align*}& v^2 = {v_1}^2 + 3{v_2}^2 \\& 6{v_2}^2 + 6v_1v_2 = 0\end{align*}\right.$$

$$\left\{\begin{align*}& v^2 = {v_1}^2 + 3{v_2}^2 \\& v_2 + v_1 = 0\end{align*}\right.$$

$$\left\{\begin{align*}& v^2 = 4{v_2}^2 \\& v_2 = -v_1\end{align*}\right.$$

$$\left\{\begin{align*}& v_1 = \frac{1}{2}v \\& v_2 = -\frac{1}{2}v\end{align*}\right.$$

b. Nel caso di urto perfettamente anelastico si conserva soltanto la quantità di moto e le due sfere si attaccano formando un unico corpo. L’equazione in questo caso è unica:

\(mv=(m+3m){{v}_{1}}\) \(\Rightarrow \) \({{v}_{1}}=\frac{1}{4}v\)

L’energia prima dell’urto vale \(K=\frac{1}{2}m{{v}^{2}}\)

L’energia dopo dell’urto diventa: \({{K}_{1}}=\frac{1}{2}\left( m+3m \right){{v}_{1}}^{2}=\frac{1}{8}m{{v}^{2}}\)

L’energia persa nell’urto è pari alla variazione di energia cinetica tra l’istante prima dell’urto e l’istante successivo all’urto:

\(\Delta K=K-{{K}_{1}}=\frac{3}{8}m{{v}^{2}}\)

Soluzione Quesito 8 – Simulazione 28 Febbraio 2019

Il flusso del campo magnetico attraverso la spira vale:

\({{\Phi }_{B}}={{l}^{2}}B(t)\)

La forza elettromotrice indotta è data dalla legge di Faraday-Neumann-Lenz e vale

\(fem=-\frac{\partial }{\partial t}{{\Phi }_{B}}=-{{l}^{2}}\frac{\partial }{\partial t}B(t)=-{{l}^{2}}{{B}_{0}}\omega \cos (\omega t)\)

La forza elettromotrice si misura in Volt (V). La corrente indotta invece può essere calcolata mediante la legge di Ohm e vale:

\(i(t)=\frac{fem}{R}=-\frac{{{l}^{2}}{{B}_{0}}\omega }{R}\cos (\omega t)\)

La corrente si misura in Ampere (A).

Inoltre per quanto riguarda le altre grandezze in gioco, abbiamo il campo di induzione magnetico \(\vec{B}\) che si misura in Tesla (T), la resistenza si misura in Ohm (Ω), il flusso magnetico si misura in Weber (Wb), il lato del circuito si misura in metri (m), la pulsazione ω si misura in rad/s.