| SIMBOLO | NOME | LaTeX | DESCRIZIONE |
| \(x\to x_0\) | x tendente a \(x_0\) | x\to x_0 | Equivale a dire che x è una quantità indefinitamente vicina a \(x_0\) |
| \(x\to x_0^+\) | x tendente ad \(x_0\) da destra | x\to x_0^+ | Equivale a dire che x è una quantità indefinitamente vicina a \(x_0\) e allo stesso tempo che \( x<x_0\) |
| \(x\to x_0^-\) | x tendente ad \(x_0\) da sinistra | x\to x_0^- | Equivale a dire che x è una quantità indefinitamente vicina a \(x_0\) e allo stesso tempo che \( x>x_0\) |
| \(\lim_{x\to x_0}f(x)\) | Limite per x che tende a un numero della funzione f(x) | \lim_{x\to x_0}f(x) | Rappresenta il limite per x che tende ad \(x_0\) della funzione f(x). Non è detto che esiste e se esiste esso è unico. |
| \(\lim_{x\to +\infty}f(x)\) | Limite per x che tende a +infinito della funzione f(x) | \lim_{x\to +\infty}f(x) | Rappresenta il limite per x che tende a \( +\infty\) della funzione f(x). Non è detto che esiste e se esiste esso è unico. |
| \(f(x)\sim_{x\to x_0}g(x)\) | Equivalenza asintotica tra la funzione f(x) e la funzione g(x) per 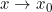 | f(x)\sim_{x\to x_0}g(x) | Rappresenta l’equivalenza asintotica tra le funzioni f(x) e g(x) quando x tende a \(x_0\)(simbolo di Landau). Equivale a dire che \( \lim_{x\rightarrow x_0}\frac{f(x)}{g(x)}=1\) , e che quindi le funzioni f(x) e g(x) hanno lo stesso comportamento in prossimità di \(x_0\) |
| \(\Theta(f(x))\) | Theta-grande di f(x) | \Theta(f(x)) | Theta-grande di f(x) rappresenta una classe di funzioni di ordine superiore ad f(x) per \( x\rightarrow x_0 \) (che deve essere sempre specificato, altrimenti il simbolo perde di significato matematico). E’ uno dei simboli di Landau |
| \(o(f(x))\) | o-piccolo di f(x) | o(f(x)) | o-piccolo di f(x) rappresenta una classe di funzioni di ordine inferiore ad f(x) per \( x\rightarrow x_0 \) (che deve essere sempre specificato, altrimenti il simbolo perde di significato matematico). E’ uno dei simboli di Landau (Edmund Georg Hermann Landau (Berlino, 14 febbraio 1877 – Berlino, 19 febbraio 1938)) |
| \(O(f(x))\) | O-grande | O(f(x)) | Theta-grande di f(x) rappresenta una classe di funzioni di ordine superiore o uguale ad f(x) per \( x\rightarrow x_0 \) (che deve essere sempre specificato, altrimenti il simbolo perde di significato matematico). E’ uno dei simboli di Landau |
| \(\Omega(f(x))\) | Omega grande | \Omega(f(x)) | Omega-grande di f(x) rappresenta una classe di funzioni di ordine superiore ad f(x) in un intorno finito di \(x_0\). E’ uno dei simboli di Landau |
| \( f(x)\asymp(g(x))\) | Equigrandezza tra f(x) e g(x) | f(x)\asymp(g(x)) | E’ uno dei simbolo di Landau che sta ad indicare che per \( x\rightarrow x_0\), le funzioni f(x) e g(x) sono equigrandi, ovvero \( \lim_{x\rightarrow x_0}\frac{f(x)}{g(x)}=l\) |