| SIMBOLO | NOME | LaTeX | DESCRIZIONE |
| \(\sum_{n=1}^{N}a_n\) | Sommatoria per n che varia da 1 a N di 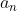 | \sum_{n=1}^{N}a_n | Rappresenta la somma dei primi N termini di una successione e cioè è come scrivere \( \sum_{n=1}^{N}a_n=a_1+a_2+..+a_N\). |
| \(\sum_{n=1}^{+\infty}a_n\) | Serie numerica | \sum_{n=1}^{+\infty}a_n | Rappresenta una serie numerica, ovvero la sommatoria degli infiniti termini di una successione. |
| \(\prod_{n=1}^{N}a_n\) | Produttoria per n che varia da 1 a N di 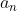 | \prod_{n=1}^{N}a_n | Rappresenta la produttoria dei primi N termini di una successione e cioè equivale a scrivere \(\prod_{n=1}^{N}a_n=a_1\cdot a_2\cdot ..\cdot a_N\). Naturalmente è sufficiente che un solo elemento della successione sia nullo per annullare l’intera produttoria |
| \(\prod_{n=1}^{+\infty}a_n\) | Produttoria infinita | \prod_{n=1}^{+\infty}a_n | Rappresenta la produttoria di tutti i termini i termini di una successione. |