Sottoinsiemi propri ed impropri di un insieme

Sottoinsiemi propri ed impropri

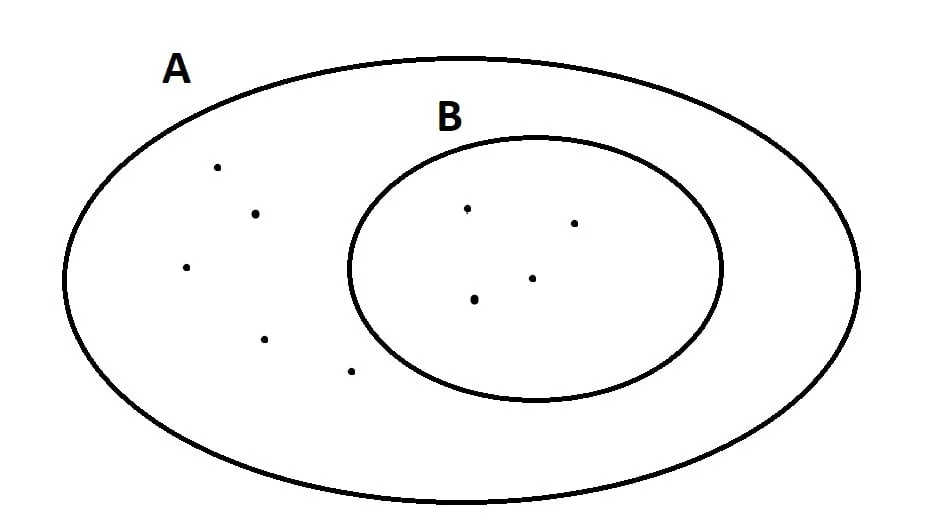
Dato un insieme A diremo che B è un sottoinsieme proprio di A se B è contenuto strettamente in A  (in formule  ) e B è non vuoto. In altre parole un sottoinsieme improprio è un qualunque sottoinsieme non vuoto di A che contiene almeno un elemento in meno rispetto a B, in modo da essere contenuto strettamente in A.

Un sottoinsieme B dell’insieme A invece si dice improprio quando non è un sottoinsieme proprio, ovvero se è vuoto oppure essattamente uguale ad A.

A questo punto proseguiamo la lezione con alcuni esempi per comprendere meglio e diamo una definizione di sottoinsieme.

Come si definisce un sottoinsieme

Diciamo che B è un sottoinsieme di A e si scrive   se tutti gli elementi di B sono contenuti anche in A. In formule possiamo scriverlo in questo modo

tutti gli elelementi di B sono anche elementi di A.

Ad esempio dato l’insieme , sono suoi sottoinsiemi ,   e .  In particolare l’insieme C coincide con A ed è lo stesso un suo sottoinsieme. D è l’insieme vuoto, cioè non contiene elementi. Possiamo dire che un insieme vuoto è contenuto e allo stesso tempo esterno a qualunque insieme, compreso se stesso.

Non sono sottoinsiemi di A,   ed  perchè entrambi contengono almeno un elemento che non è contenuto in A.

Esempi di sottoinsiemi propri e impropri

Un sottoinsieme proprio di un insieme A è un qualunque sottoinsieme contenuto strettamente nell’insieme A e non vuoto

Vediamo con l’esempio di prima:

Dato ,  è un sottoinsieme proprio ,  mentre non sono sottoinsiemi propri gli insiemi e 

C non è un sottoinsieme proprio perchè coincide con A, esso è pertanto un sottoinsieme improrio.

D non è un sottoinsieme proprio perchè è vuoto, esso è pertanto un sottoinsieme improprio.

B è un sottoinsieme proprio di A perchè contiene almeno un elemento che non è contenuto in A, cioè il numero 5.

Dato un qualunque insieme, gli unici sottoinsiemi impropri sono se stesso e l’insieme vuoto

Naturalmente l’insieme vuoto ammette solo sottoinsiemi impropri, infatti l’unico sottoinsieme dell’insieme vuoto è se stesso, che è vuoto e quindi per definizione è improprio.

Insieme infinito definito con il concetto di sottoinsieme proprio

E’ possibile ridefinire il concetto di insieme infinito attraverso il concetto di insiemi propri e impropi. Infatti è possibile dire che nella teoria degli insiemi un insieme A si dice infinito se ogni suo sottoinsieme finito è un sottoinsieme proprio.

E’ facile immaginare che se prendiamo un qualunque insieme finito, tra i suoi sottoinsiemi c’è se stesso che è un sottoinsieme improprio. Mentre se prendiamo un insieme infinito, e un qualunque suo sottoinsieme finito sicuramente non può essere un sottoinsieme improprio, perchè un insieme finito non può coincidere con un insieme infinito.